Only Stars Approximately 10 Times or More the Mass of Our Sun Can:
Chief Sequence Stars

Credit: NASA
The Dominicus
The bulk of stars in the galaxy, including our Sun, Sirius and Alpha Centauri A and B are all master sequence stars. The Sunday's relative longevity and stability have provided the conditions necessary for life to evolve here on Earth. Our agreement of the processes involved and characteristics of this key group of stars has progressed in parallel with our understanding of nuclear physics.
- Backdrop of Chief Sequence Stars
- Hydrostatic Equilibrium
- Stellar Mass
- Main Sequence Lifespan
- Composition
- Table of Properties
- Nucleosynthesis and Fusion Reactions
- Proton-Proton Chain
- CNO Cycle
- Lord's day's Main Sequence Lifespan
- Energy Transport in a Star
Properties of Main Sequence Stars
Main sequence stars are characterised by the source of their free energy. They are all undergoing fusion of hydrogen into helium inside their cores. The rate at which they exercise this and the amount of fuel available depends upon the mass of the star. Mass is the key cistron in determining the lifespan of a main sequence star, its size and its luminosity. Stars on the main sequence also appear to exist unchanging for long periods of time. Any model of such stars must be able to account for their stability.
Hydrostatic Equilibrium
The simple model of whatsoever primary sequence star is of a dense gas/fluid in a state of hydrostatic equilibrium. The inwards acting force, gravity, is balanced by outward acting forces of gas pressure and the radiation force per unit area. Apart from the extremely hot but tenuous corona , the pressure level and temperature of stars basically increases as you arroyo the core.
Main sequence stars essentially have a fixed size that is a function of their mass. The more than massive the star, the greater its gravitational pull inwards. This in turn compresses the gas more than. As you try and compress a gas it exerts a gas pressure back, information technology resists the pinch. In stars this gas pressure lonely is non sufficient to withstand the gravitational plummet. Once the cadre temperature has reached well-nigh 10 one thousand thousand K, fusion of hydrogen occurs, releasing energy. This free energy exerts an outwards radiation pressure due to the action of the photons on the extremely dense thing in the core. The radiations pressure combined with the gas pressure level balances the inwards pull of gravity preventing further collapse.
Stellar Mass
As was apparent from the evolutionary Hayashi tracks on the previous folio, a star's position on the main sequence its really a role of its mass. This is an incredibly useful relationship, called the mass-luminosity relation. If we know where on the primary sequence a star is nosotros can infer its mass. In general the more than massive a star is, the further up the main sequence it is found and the more luminous information technology is. Mathematically this relation is expressed by:
log(Fifty/LSun )= northward log(Yard/ThousandSun ) or
Fifty/50Sunday = (M/MSunday ) north (Equation half-dozen.1)
where n is well-nigh iv for Sun-like stars, 3 for the more massive stars and 2.5 for dim blood-red main sequence stars. (*Notation this formula is not required for HSC exams). A 0.1 solar mass star has just about one-thousandth the luminosity of the Lord's day whereas a 10-solar mass star is has a luminosity 10,000 × that of our Sun.
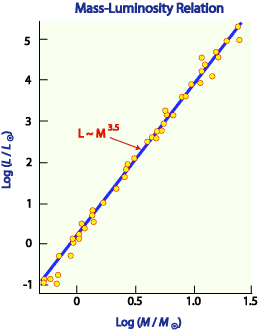
The lower mass limit for a master sequence star is about 0.08 that of our Sunday or 80 times the mass of Jupiter. Below this mass the gravitational forcefulness inward is insufficient to generate the temperature needed for core fusion of hydrogen and the "failed" star forms a brownish dwarf instead. The first such object discovered in 1995 was Gliese 229B at 0.05 solar masses.
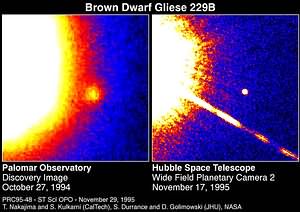
Gliese 229B, the first brownish dwarf, discovered in 1995.
Limits on the upper mass of stars is thought to be somewhere between 150 and 200 solar masses based on theoretical modeling. Such stars are extremely rare and short-lived.
The greater the mass of a chief sequence star, the greater its constructive temperature. This, combined with the larger radius of higher mass main sequence stars accounts for their much greater luminosity. Remember, L ∝ T 4 and L ∝ R 2 so fifty-fifty a minor increase in constructive temperature will significantly increase luminosity.
Master-Sequence Lifespan
The main sequence is the stage where a star spends virtually of its beingness. Relative to other stages in a star'due south "life" it is extremely long; our Lord's day took about xx 1000000 years to form but volition spend nigh 10 billion years (1 × 1010 years) equally a main sequence star before evolving into a blood-red giant. What determines the primary sequence lifespan of a star?
Master sequence stars vary in mass. You may imagine that a more massive star has more fuel available so tin spend more time on the master sequence fusing hydrogen to helium. You would be wrong - the opposite is truthful. More massive stars have a stronger gravitational strength acting inwards so their core gets hotter. The college temperatures hateful that the nuclear reactions occur at a much greater charge per unit in massive stars. They thus apply upwards their fuel much quicker than lower mass stars. This is coordinating to the situation with many chemical reactions, the higher the temperature the faster the reaction rate.
Lifespans for main sequence stars have a vast range. Whilst our Sun will spend x billion years on the master sequence, a high-mass, ten solar-mass (10Yard Sunday) star volition only last 20 million years (two.0× 10seven years) on the main sequence. A star with a only half the mass of Sun can spend 80 billion years on the primary sequence. This is much longer than the historic period of the Universe which means that all the low-mass stars that have formed are still on the main sequence - they accept not had fourth dimension to evolve off it.
Key Properties of Main Sequence Stars
| Mass/Yard Sun | Luminosity/L Sun | Effective Temperature (Chiliad) | Radius/R Sun | Main sequence lifespan (yrs) |
|---|---|---|---|---|
| 0.10 | 3×10-3 | 2,900 | 0.xvi | 2×x12 |
| 0.fifty | 0.03 | 3,800 | 0.half dozen | two×1011 |
| 0.75 | 0.3 | v,000 | 0.8 | 3×ten10 |
| 1.0 | 1 | vi,000 | 1.0 | 1×1010 |
| one.5 | v | seven,000 | i.4 | two×10nine |
| 3 | 60 | xi,000 | 2.5 | two×108 |
| 5 | 600 | 17,000 | 3.viii | vii×107 |
| 10 | x,000 | 22,000 | v.6 | 2×10seven |
| 15 | 17,000 | 28,000 | vi.8 | 1×10seven |
| 25 | 80,000 | 35,000 | 8.vii | 7×ten6 |
| 60 | 790,000 | 44,500 | 15 | 3.four×106 |
Composition
Although at that place are 92 naturally occurring elements and a few hundred isotopes, the composition of stars is remarkably similar and unproblematic. Stars are composed almost entirely of hydrogen and helium. A star such as our Sun is nigh 73% hydrogen by mass and 25% helium. If adamant by number of nuclei and so it is 92% hydrogen and seven.viii% helium. The remaining 2% past mass or 0.2% past number is all the heavier elements. Historically astronomers termed these elements with diminutive numbers greater than 2 every bit metals. These include elements such as carbon and oxygen. The use of "metals" is not to exist confused with the more common chemical meaning of the term.
Metallicity is a measure out of the abundance of elements heavier than helium in a star and is expressed equally the fraction of metals by mass. It tin be adamant or at least inferred from spectroscopic and photometric observations. In general stars with higher metallicities are inferred to be younger than those with very low values. This is due to the fact that elements heavier than helium are fabricated inside stars past nucleosynthesis and released into interstellar space past mass-loss events such as supernova explosions in the late stages of stellar evolution. Early generations of stars
Stars found in the screw arms of galaxies, including our Sun, are generally younger and have high metallicities. They are referred to as Population I stars. Population Ii stars are older, cerise stars with lower metallicities and are typically located in globular clusters in galactic halos, in elliptical galaxies and about the galactic center of screw galaxies.
Nucleosynthesis and Fusion Reactions
Nucleosynthesis simply refers to the production of nuclei heavier than hydrogen. This occurs in chief sequence stars through ii primary processes, the proton-proton chain and the CNO cycle (carbon, nitrogen, oxygen). Primordial nucleosynthesis occurred very early in the history of the Universe, resulting in some helium and small traces of lithium and deuterium, the heavy isotope of hydrogen. Fusion processes in postal service-principal sequence stars are responsible for many of the heavier nuclei. Other mechanisms such as neutron capture also occur in the last stages of massive stars. Both discussed in later pages.
Primary sequence stars fuse hydrogen into helium within their cores. This is sometimes chosen "hydrogen called-for" only you lot need to be careful with this term. "Burning" implies a combustion reaction with oxygen but the process within stellar cores is a nuclear reaction, not a chemical one.
The nuclear fusion in the cores of main sequence stars involves positive hydrogen nuclei, ionised hydrogen atoms or protons, to slam together, releasing energy in the procedure. At each stage of the reaction, the combined mass of the products is less than the total mass of the reactants. This mass difference is what accounts for the free energy released according to Einstein's famous equation: Eastward = chiliad c2 where Due east is the energy, thousand the mass and c the speed of light in a vacuum. This is better expressed every bit:
Due east = Δg ctwo where Δk is the alter in mass. (Equation 6.two)
In weather condition such every bit those on Globe, if nosotros effort to bring two protons (hydrogen nuclei) together the electrostatic interaction tends to crusade them to repel. This coulombic repulsion must exist overcome if the protons are to fuse. The actual process whereby 2 protons can fuse involves a quantum mechanical effect known equally tunneling and in practice requires the protons to have extremely high kinetic energies. This means that they must exist traveling very fast, that is have extremely high temperatures. Nuclear fusion only starts in the cores of stars when the density in the core is great and the temperature reaches about 10 1000000 K.
In that location are two master processes by which hydrogen fusion takes identify in main sequence stars - the proton-proton chain and the CNO (for carbon, nitrogen, oxygen) cycle.
Proton-Proton (pp) Concatenation
The main process responsible for the energy produced in most principal sequence stars is the proton-proton (pp) chain. It is the dominant procedure in our Sun and all stars of less than 1.5 solar masses. The net effect of the process is that 4 hydrogen nuclei, protons, undergo a sequence of fusion reactions to produce a helium-4 nucleus. The sequence shown beneath is the near common course of this chain and is too called the ppI concatenation. It accounts for 85% of the fusion energy released in the Sunday.
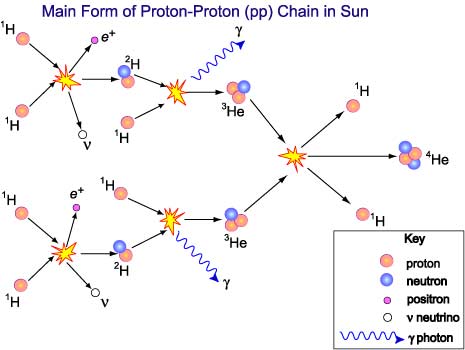
If you report the diagram above you will annotation that half-dozen protons are used in the series of reactions but ii are released back. Other products include the He-4 nucleus, 2 neutrinos, two high-energy gamma photons and 2 positrons. Each of these products carries some of the free energy released from the slight reduction in full mass of the system. The overall reaction tin can be summarised as:
ppI: 4H-i → He-4 + 2e+ + 2ν + 2γ
The neutrinos are neutral and accept extremely low rest masses. They essentially do not interact with normal matter and then travel straight out from the core and escape from the star at virtually the speed of lite. About 2% of the free energy released in the pp concatenation is carried past these neutrinos.
Positrons are the antiparticle of electrons. Although the pp chain involves the fusion of hydrogen nuclei, the cores of stars still contain electrons that accept been ionised or ripped off from their hydrogen or helium nuclei. When a positron collides with an electron, an antimatter-matter event occurs in which each annihilates the other, releasing yet more high-energy gamma photons.
2 other forms of the pp chain tin occur in stars and contribute about 15% of the energy production in the Sun. In the ppII chain, a He-iii nucleus produced via the showtime stages of the ppI chain undergoes fusion with a He-4 nucleus, producing Exist-7 and releasing a gamma photon. The Be-7 nucleus then collides with a positron, releasing a neutrino and forming Li-7. This in turn fuses with a proton, splitting to release two He-4 nuclei. A rarer consequence is the ppIII chain whereby a Be-7 nucleus produced equally above fuses with a proton to grade B-8 and release a gamma photon. B-8 is unstable, undergoing beta positive disuse into Be-viii, releasing a positron and a neutrino. Be-eight is also unstable and splits into ii He-4 nuclei. This process only contributes 0.02% of the Sunday'south energy. These forms are summarised equally:
ppII: 4H-i + due east- → He-4 + e+ + 2ν + 2γ
ppIII: 4H-1 → He-4 + 2e+ + 2ν + 3γ
CNO Bike
Stars with a mass of most 1.five solar masses or more produce well-nigh of their energy past a unlike form of hydrogen fusion, the CNO wheel. CNO stands for carbon, nitrogen and oxygen equally nuclei of these elements are involved in the process. As its proper noun implies, this process is cyclical. It requires a proton to fuse with a C-12 nuclei to outset the cycle. The resultant Northward-13 nucleus is unstable and undergoes beta positive decay to C-xiii. This then fuses with another proton to from N-14 which in plow fuses with a proton to requite O-15. Being unstable this undergoes beta positive decay to form Due north-fifteen. When this fuses with a proton, the resultant nucleus immediately splits to form a He-4 nucleus and a C-12 nucleus. This carbon nucleus is then able to initiate another cycle. Carbon-12 thus acts like a nuclear catalyst, it is essential for the procedure to proceed just ultimately is not used up by it.
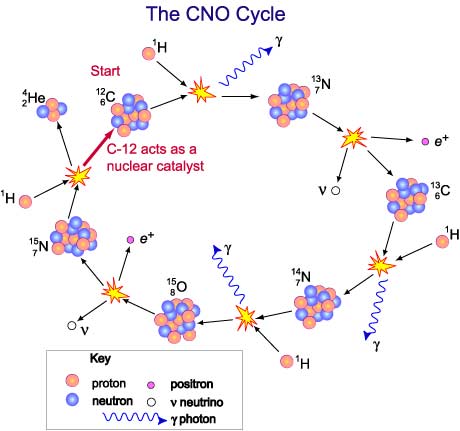
As with the various forms of the pp chain, gamma photons and positrons are released in the bike forth with the final helium and carbon nuclei. All these possess energy. The overall reaction can be summarised every bit:
CNO: 4H-1 → He-4 + 2e+ + 2ν + 3γ
Why does the CNO bicycle dominate in college-mass stars? The respond has to do with temperature. The first phase of the pp concatenation involves two protons fusing together whereas in the CNO cycle, a proton has to fuse with a carbon-12 nucleus. As carbon has 6 protons the coulombic repulsion is greater for the offset footstep of the CNO cycle than in the pp chain. The nuclei thus require greater kinetic energy to overcome the stronger repulsion. This means they have to have a college temperature to initiate a CNO fusion. Higher-mass stars take a stronger gravitational pull in their cores which leads to higher core temperatures.
The CNO cycle becomes the chief source of energy in stars of 1.5 solar masses or higher. Cadre temperatures in these stars are 18 million K or greater. As the Lord's day's core temperature is most 16 one thousand thousand K, the CNO cycle accounts for only a infinitesimal fraction of the total energy released. The relative free energy produced past each process is shown on the plot beneath.
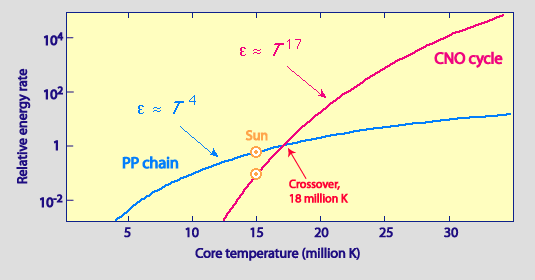
Credit: Adapted from an prototype by Mike Guidry, Academy of Tennessee.
Relative energy production for the pp chain and CNO cycle. Notation that at the temperature range typically found in main sequence stars, the contribution due to the pp concatenation is dependent on T 4 whereas that from the CNO cycle is T 17. In a higher place eighteen million Chiliad the CNO cycle contributes almost of the free energy and whatsoever further slight increase in core temperature leads to a greater increase in energy output.
As we have already seen, the Sun has a chief sequence lifespan of virtually 10 billion (1 × 10x) years. How practice astronomers calculate such a value? A first order approximation for this value is surprisingly piece of cake to derive.
You volition remember that the mass of a helium-4 nucleus is slightly less than the sum of the four separate protons needed to course it. In nuclear physics, the masses dealt with are so small that the atomic mass unit or amu is used instead of the kilogram where 1 amu = i.66 × 10-27 kg. A proton has a mass of 1.0078 amu then 4 protons add together up to 4.0312 amu. A helium-iv nucleus has a mass of 4.0026 which ways that the mass defect, the difference between the two total masses, is 0.0286 amu or simply 0.7%. From equation 6.2:
East = Δone thousand ctwo and so substituting in values gives
Due east = 0.0286(i.66 × 10-27)(3 × 108)2
∴ E = 4.3 × 10-12 J
The production of each helium nucleus releases merely a small amount of energy, x-12 J which does not seem a lot. We know though measurement that the Sun's luminosity is 3.90 × x26 J.southward-1. To produce this amount of energy, vast numbers of helium, (3.90 × 1026)/(4.three × 10-12) = 9 × 1037, must exist formed every 2nd. Each 2nd, 600 million tons of hydrogen fuse to form 596 million tons of helium. This means 4 million tons of matter is destroyed and converted into energy each second.
The high temperature needed for hydrogen fusion is only found in the core region of the Lord's day. This comprises only about x% of its total mass. The energy potentially available from this mass of hydrogen is roughly:
Due easttotal = (mass defect per He nucleus produced) × c 2 × (mass of H in core)
∴ Eastfull = 0.0071(9 × 10xvi)(0.1 × two.0 × 1030)
= i.28 × 1044 J
Given that the Sun'southward energy output is currently 3.ninety × x26 J. due south-1 and assuming that it will be roughly constant for its principal sequence lifespan, then the Lord's day has enough core hydrogen for about ten billion years. As it is currently about virtually 5 billion years erstwhile this means information technology is half fashion through its main sequence life.
We have now seen how energy is produced in a star such as the Sun. How, though, does this energy escape from the star? 2 processes, radiations and convection, play a vital function.
The Sun's interior comprises three main regions. The core, simply 25% of the Sun's diameter, a radiative zone extending from the core to lxx% of the diameter and the outer region where convection processes boss.
High-free energy gamma photons produced in the core do not escape easily from it. The high temperature plasma in the core is about x times denser than a dense metal on Earth. A photon tin only travel a centimeter or so on average in the cadre before interacting with and scattering from an electron or positive ion. Each of these interactions changes both the free energy and travel direction of the photon. The management a photon travels later on an interaction is random so sometimes it is reflected back into the core. Nevertheless over many successive interactions the internet event is that the photon gradually makes its way out from the core. The path it takes is called a random walk. Photons lose free energy to the electrons and ions with each interaction creating a range of photon energies. This procedure is known equally thermalisation and results in the feature blackbody spectrum that forms the continuum groundwork spectrum of stars.
Interactions between ions and electrons also produce many additional photons of diverse energies. These too contribute to the blackbody spectrum.
The electrons and nuclei formed in fusion reactions as well deport kinetic free energy that they tin can impart to other particles through interactions, raising the thermal free energy of the plasma. Neutrinos produced by the diverse fusion and disuse reactions travel out from the core at nearly the speed of light. They are effectively unimpeded by the dense matter in the core of master sequence stars. They bear away well-nigh ii% of the total energy.
The outer 30% of the Sun is at lower temperature and density than the inner parts. Here, convection currents are responsible for transporting energy to the surface. Deep cells, 30,000 km across are responsible for supergranulation. The cells just beneath the photosphere are but 1,000 km across and are responsible for the granulation seen on the surface of the Sunday equally in the image below.
What happens when a main sequence star runs out of hydrogen, the fuel in its cadre? This leads us to evolution off the main sequence which is discussed on the next folio.
Source: https://www.atnf.csiro.au/outreach/education/senior/astrophysics/stellarevolution_mainsequence.html
0 Response to "Only Stars Approximately 10 Times or More the Mass of Our Sun Can:"
Post a Comment